The Mathematical Soul of Transformers: How Linear Algebra Changed Everything

When I first encountered the Transformer architecture back in 2017, I remember thinking it was almost too elegant to be real. Here was this mathematical framework that would eventually power ChatGPT, revolutionize how we interact with AI, and fundamentally change our relationship with technology. Yet at its core, it's "just" matrix multiplication, attention mechanisms, and some clever applications of calculus and linear algebra.

But that's like saying Beethoven's 9th Symphony is "just" vibrations in the air.

The magic of Transformers isn't in any single mathematical concept—it's in how brilliantly these mathematical building blocks work together to create something that can understand context, generate coherent text, and even reason about complex problems. Today, I want to take you on a journey through the mathematical soul of these remarkable systems.

Why Math Matters More Than You Think

Before we dive into the intricate world of Transformers, let's address the elephant in the room: why should you care about the math behind AI?

I've noticed that many people approaching AI fall into two camps. The first group gets so caught up in the mathematical complexity that they lose sight of the bigger picture. The second group treats AI as a complete black box, missing out on the profound insights that come from understanding how these systems actually work.

The truth is, understanding the mathematical foundations of Transformers doesn't just make you a better AI practitioner—it fundamentally changes how you think about intelligence itself.

The Mathematical Foundation: More Than Just Numbers

Linear Algebra: The Language of AI

When people ask me what single mathematical concept is most important for understanding modern AI, my answer is always the same: linear algebra. Not because it's the most complex, but because it's the most fundamental.

Think about it this way: every piece of text that goes into a Transformer gets converted into vectors—mathematical objects that exist in high-dimensional space. When ChatGPT "understands" the word "cat," it's really working with a 1,536-dimensional vector (in the case of GPT-3.5) that captures the mathematical essence of "cat-ness."

But here's where it gets interesting. These aren't arbitrary numbers. The relationships between these vectors mirror the relationships between concepts in human language. The vector for "king" minus the vector for "man" plus the vector for "woman" actually gets you close to the vector for "queen." That's not coincidence—that's linear algebra capturing the structure of human thought.

Calculus: The Engine of Learning

Here's something that blew my mind when I first understood it: every time a Transformer learns something new, it's essentially solving a massive calculus optimization problem.

During training, the model looks at billions of examples and asks: "How should I adjust my 175 billion parameters (in the case of GPT-3) to better predict the next word?" This is where calculus comes in, specifically gradient descent—a method for finding the bottom of a mathematical hill.

But we're not talking about a simple hill. We're talking about a landscape with 175 billion dimensions, where each dimension represents one parameter in the model. The mathematical elegance of backpropagation—the algorithm that calculates how to update each parameter—relies entirely on the chain rule from calculus.

Probability: Understanding Uncertainty

What many people don't realize is that Transformers are fundamentally probabilistic systems. When ChatGPT generates text, it's not deterministically choosing the "correct" next word—it's calculating a probability distribution over all possible next words and sampling from that distribution.

This probabilistic nature is what gives these models their creativity and flexibility, but it's also what makes them occasionally unpredictable. Understanding concepts like probability distributions, maximum likelihood estimation, and Bayesian inference is crucial for working effectively with these systems.

The 2017 Revolution: "Attention Is All You Need"

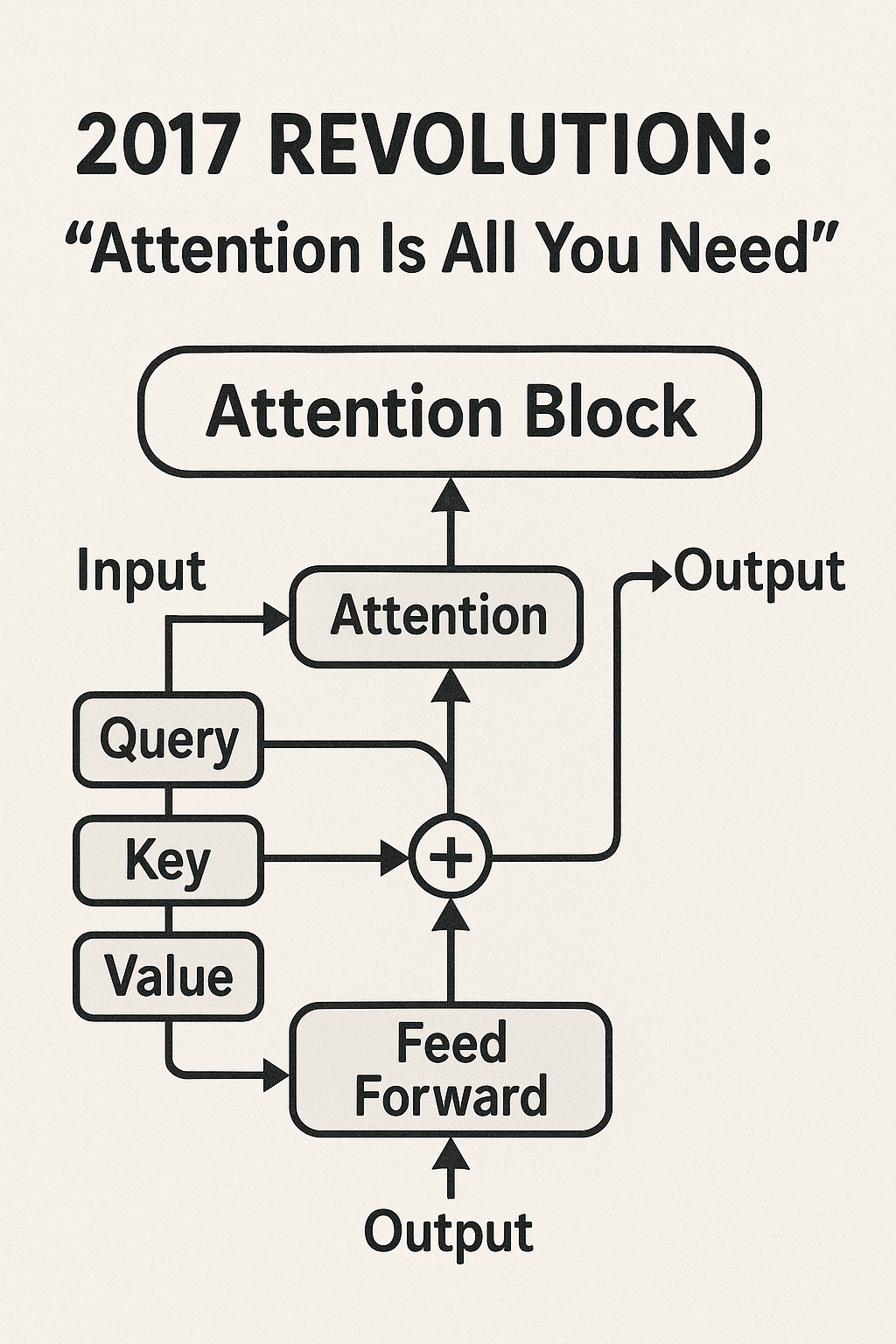
The paper that changed everything had one of the most confident titles in the history of computer science: "Attention Is All You Need." The authors weren't just proposing a new architecture—they were making a bold mathematical claim about how intelligence could be modeled.

The Brilliance of Self-Attention

Before Transformers, processing sequential data like text required processing words one at a time, from left to right. This was like trying to understand a symphony by listening to one note at a time, never being able to hear the harmonies or the overall structure.

The attention mechanism changed all that. Suddenly, every word in a sentence could "attend" to every other word simultaneously. But how does this work mathematically?

The magic happens through three matrices: Query (Q), Key (K), and Value (V). Here's the intuition:

• Query: "What am I looking for?"
• Key: "What do I have to offer?"
• Value: "Here's my actual content"

For each word, the model computes attention scores by taking the dot product of the query with all the keys. These scores get passed through a softmax function (which ensures they sum to 1), creating a probability distribution that determines how much each word should "attend" to every other word.

But this simplicity is misleading. This single equation enables the model to capture complex relationships like:

• Pronoun resolution ("The cat chased its tail" - "its" refers to "cat")
• Long-range dependencies ("The keys to the car that I bought yesterday are missing")
• Hierarchical structure (understanding that "quickly" modifies "ran" in "The dog ran quickly")

Multi-Head Attention: Parallel Processing of Meaning

One of the most elegant aspects of the Transformer architecture is multi-head attention. Instead of having a single attention mechanism, the model runs multiple attention "heads" in parallel, each focusing on different types of relationships.

Think of it like having multiple experts examining the same sentence:

• Head 1 might focus on syntactic relationships (subject-verb-object)
• Head 2 might capture semantic similarity
• Head 3 might track discourse markers and logical flow

Mathematically, each head learns its own Q, K, and V matrices, allowing it to attend to different aspects of the input. The outputs are then concatenated and projected through another linear layer, combining all these different perspectives into a single representation.

Positional Encoding: Teaching Math to Understand Order

Here's a problem that stumped researchers for years: how do you teach a mathematical system that processes everything in parallel to understand the order of words?

The Transformer's solution is positional encoding—a brilliant mathematical trick that injects information about word position directly into the vector representations. The original paper used sinusoidal functions with different frequencies:

PE(pos, 2i) = sin(pos/10000^(2i/d_model))
PE(pos, 2i+1) = cos(pos/10000^(2i/d_model))

This isn't arbitrary mathematical complexity—it's a carefully designed system that allows the model to learn relative positions and extrapolate to longer sequences than it was trained on.

From Research to Reality: The GPT Evolution

The journey from the original Transformer paper to modern systems like GPT-4 represents one of the most remarkable scaling stories in the history of computer science. But it's not just about making things bigger—it's about mathematical innovations that make scaling possible.

The Decoder-Only Revolution

While the original Transformer used both an encoder and decoder, the GPT family made a crucial architectural decision: use only the decoder portion, but scale it massively. This might seem like a simplification, but it's actually a profound insight about the nature of language modeling.

By training a massive decoder-only model to predict the next word in text, researchers discovered they could create a system capable of:

• Translation (by learning patterns from multilingual text)
• Summarization (by learning from examples in the training data)
• Code generation (by training on code repositories)
• Reasoning (by learning from mathematical and logical text)

The Mathematics of Scale

One of the most important discoveries in modern AI is the relationship between model size, training data, and performance. This isn't just empirical observation—it follows mathematical scaling laws that were first formalized by researchers at OpenAI.

These scaling laws suggest that model performance improves predictably with:

• Model size (number of parameters)
• Training data (number of tokens)
• Compute budget (floating-point operations)

The mathematical relationship is approximately:

Where α, β, and γ are constants that can be empirically determined. Understanding these relationships has been crucial for planning the development of increasingly powerful models.

Advanced Techniques: Pushing Mathematical Boundaries

Retrieval Augmented Generation (RAG): Mathematical Memory

One of the most significant developments in making LLMs more practical is RAG—Retrieval Augmented Generation. The mathematical insight here is profound: instead of trying to memorize all knowledge in the model's parameters, we can teach the model to search through external databases and incorporate that information into its reasoning.

The process relies heavily on vector similarity. Documents are embedded into the same high-dimensional space as the model's internal representations, and relevant information is retrieved using similarity measures like cosine similarity:

This allows the model to access up-to-date information and specific knowledge without retraining—a mathematical solution to the knowledge cutoff problem.

Mixture of Experts: Specialized Mathematical Brains

Modern systems like Grok-4 implement Mixture of Experts (MoE) architectures, where different "expert" networks specialize in different types of problems. This isn't just an engineering trick—it's a mathematical insight about how to scale intelligence efficiently.

Instead of activating all 2.4 trillion parameters for every computation, MoE models use a gating network to route inputs to the most relevant experts. This allows for massive model capacity while keeping computational costs manageable.

Test-Time Compute Scaling: Mathematical Reflection

Perhaps the most exciting recent development is test-time compute scaling—the ability to improve model performance by spending more computational resources during inference. This is like giving the model time to "think" about difficult problems.

Systems like GPT-5's "smart router" decide when to activate test-time compute based on problem difficulty. For complex reasoning tasks, the model might:

• Generate multiple candidate solutions
• Use specialized verification models to score them
• Iteratively refine the best candidates
• Apply techniques like Monte Carlo Tree Search for structured reasoning

This represents a fundamental shift from viewing inference as a single forward pass to seeing it as an iterative reasoning process.

The Human Element: Why Mathematical Intuition Matters

Throughout this exploration, I've tried to emphasize that understanding the mathematics of Transformers isn't just academic exercise—it's practical wisdom that changes how you work with these systems.

When you understand that attention mechanisms are computing similarity in vector space, you start to think differently about prompt engineering. When you grasp that the model is sampling from probability distributions, you begin to understand why temperature and top-p parameters matter so much.

Most importantly, when you see how mathematical principles like linear algebra and calculus combine to create apparent intelligence, you gain a deeper appreciation for both the power and limitations of these systems.

Looking Forward: The Mathematical Frontier

As I write this, the field of AI is moving faster than ever. New architectural innovations, scaling discoveries, and mathematical insights emerge weekly. But the foundational principles we've explored—linear algebra, calculus, probability, and the attention mechanism—remain central to everything we're building.

The next breakthroughs will likely come from:

• Better mathematical frameworks for reasoning and planning
• More efficient architectures that achieve the same capabilities with less computation
• Novel training objectives that better align models with human values and intentions
• Hybrid systems that combine neural networks with symbolic reasoning

What excites me most is that we're still in the early days. The mathematical foundations we've built are solid, but there's so much more to discover about how these principles can be combined and extended.

The Elegant Mathematics of Intelligence

As we wrap up this journey through the mathematical soul of Transformers, I want to return to something I mentioned at the beginning: the elegance of it all.

There's something profound about the fact that matrix multiplication, attention mechanisms, and gradient descent can combine to create systems that can write poetry, solve mathematical problems, and engage in meaningful conversations. It suggests that intelligence itself might be more mathematically tractable than we ever imagined.

The Transformer architecture showed us that some of the most complex aspects of human cognition—attention, memory, reasoning—can be modeled using relatively simple mathematical operations, scaled up and trained on vast amounts of data.

This doesn't diminish the mystery of intelligence; if anything, it deepens it. How is it that these mathematical relationships capture something so essentially human as language understanding? How do billions of parameters, each just a number, combine to create something that feels almost magical?

I don't have complete answers to these questions, and I suspect no one does yet. But I do know this: understanding the mathematics behind Transformers has fundamentally changed how I think about intelligence, computation, and what it means to understand.

The next time you interact with ChatGPT or any other AI system, remember that beneath the surface lies an intricate dance of mathematical operations—vectors moving through high-dimensional spaces, attention patterns weaving connections between ideas, and optimization algorithms constantly refining the model's understanding of our world.

It's mathematics, yes. But it's mathematics with a soul.

References